SOMA DOS ÂNGULOS INTERNOS DE UM POLÍGONO

Dado um polígono de n lados qual é a soma de seus n ângulos internos?

Para responder a essa pergunta vamos ver alguns casos particulares.

Triângulo – Já foi demonstrado em vários momentos que a soma dos ângulos internos de um triângulo é 180°.  Tal demonstração será omitida e deixada a cargo do leitor, por ser simples.

Quadrilátero – No caso dos polígonos seguintes adotaremos a estratégia de dividi-los em triângulos a partir de um de seus vértices. Ao se efetuar tal divisão no quadrilátero teremos dois triângulos, como mostra a figura.

E a soma dos ângulos do quadrilátero é facilmente efetuada fazendo-se a soma dos ângulos dos dois triângulos, ou seja: 2.180°=360°

Pentágono – Analogamente, no pentágono teremos três triângulos. E a soma dos ângulos do pentágono será 3.180°=540°.

Hexágono – Da mesma forma, no hexágono teremos quatro triângulos, e a soma dos ângulos será 4.180°=720°.

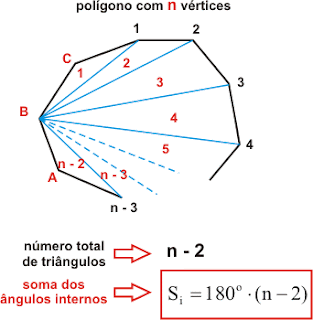
Generalizando, percebemos que o número de triângulos formados é sempre dois a menos que o número de lados do polígono, ou seja, para um polígono de n lados o número de triângulos formados será n-2, e daí:

Assim, concluímos que a soma dos ângulos internos de um polígono de n lados será dada por:

S=180°.(n-2).

Autor: Cassiano Pimho